sklearn 模型选择和评估-白红宇

sklearn 模型选择和评估

阅读量：5909 次

发布时间：2019-06-19

本文共 12448 字，大约阅读时间需要 41 分钟。

一、模型验证方法如下：

通过交叉验证得分：model_sleection.cross_val_score(estimator,X)

对每个输入数据点产生交叉验证估计：model_selection.cross_val_predict(estimator,X)

计算并绘制模型的学习率曲线：model_selection.learning_curve(estimator,X,y)

计算并绘制模型的验证曲线：model_selection.validation(estimator,...)

通过排序评估交叉验证的得分在重要性：model_selection.permutation_test_score(...)

①通过交叉验证得分：model_sleection.cross_val_score(estimator,X)

import numpy as npfrom sklearn.model_selection import cross_val_scorefrom sklearn import datasets,svmdigits=datasets.load_digits()X=digits.datay=digits.targetsvc=svm.SVC(kernel='linear')C_s=np.logspace(-10,0,10)print("参数列表长度",len(C_s))scores=list()scores_std=list()n_folds=3for C in C_s:    svc.C=C    this_scores=cross_val_score(svc,X,y,cv=n_folds,n_jobs=1)    #print(this_scores)    scores.append(np.mean(this_scores))    scores_std.append(np.std(this_scores))#绘制交叉验证的曲线import matplotlib.pyplot as pltplt.figure(1,figsize=(4,3))plt.clf()plt.semilogx(C_s,scores)plt.semilogx(C_s,np.array(scores)+np.array(scores_std),'b--')plt.semilogx(C_s,np.array(scores)-np.array(scores_std),'b--')locs,labels=plt.yticks()plt.yticks(locs,list(map(lambda x:"%g" %x,locs)))plt.ylabel("CV score")plt.xlabel("Parameter C")plt.ylim(0,1.1)plt.show()

结果图

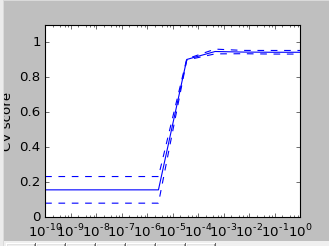
②对每个输入数据点产生交叉验证估计：model_selection.cross_val_predict(estimator,X)

from sklearn import datasets,linear_modelfrom sklearn.model_selection import cross_val_predictdisbetes=datasets.load_diabetes()X=disbetes.data[:150]y=disbetes.target[:150]lasso=linear_model.Lasso()y_pred=cross_val_predict(lasso,X,y)print(y_pred)结果：[ 174.26933996  117.6539241   164.60228641  155.65049088  132.68647979  128.49511245  120.76146877  141.069413    164.18904498  182.37394949  111.04181265  127.94311443  135.0869234   162.83066014  135.3573514  157.64516523  178.95843326  163.3919841   143.85237903  144.29748882  133.58117218  124.77928571  132.90918003  208.52927     153.61908967  154.16616341  118.95351821  163.50467541  145.89406196  168.3308101  155.87411031  123.45960148  185.70459144  133.38468582  117.2789469  150.27895019  174.1541028   160.03235091  192.31389633  161.58568256  154.2224809   119.35517679  146.15706413  133.82056934  179.68118754  137.96619936  146.07788398  126.77579723  123.32101099  166.26710247  146.41559964  161.67261029  147.47731459  138.44595305  144.85421048  113.77990664  185.54970402  115.31624749  142.23672103  171.07792136  132.5394716   177.80524864  116.5616502   134.25230846  142.88707475  173.2830912   154.31273504  149.16680759  144.88238997  121.97783103  110.38457621  180.25559631  199.06141058  151.1195546   161.14217698  153.96960812  150.77179755  113.30903579  165.15755771  115.85735727  174.19267171  150.12027233  115.47891783  153.38967232  115.31573467  156.49909623   92.62211515  178.15649994  131.59320715  134.46166754  116.97678633  190.00790119  166.01173292  126.25944471  134.29256991  144.71971963  190.9769591   182.39199466  154.45325308  148.30325558  151.72036937  124.12825466  138.6011155   137.75891286  123.0917243  131.74735403  112.07367481  124.56956904  156.78432061  128.63135591   93.68260079  130.54324394  131.8693231   154.5708257   179.81343019  165.78130755  150.04779033  162.37974736  143.92996797  143.15645843  125.20161377  145.99590279  155.3505536   145.97574185  134.66120515  163.92450638  101.92329396  139.33014324  122.71377023  152.20573113  153.36931089  116.76545147  131.96936127  109.74817383  132.57453994  159.38030328  109.31343881  147.69926269  156.3664255   161.12509958  128.16523686  156.78446286  154.04375702  124.83705022  143.85606595  143.23651701  147.76316913  154.21572891  129.07895017  157.79644923]

③、计算并绘制模型的学习率曲线：model_selection.learning_curve(estimator,X,y)

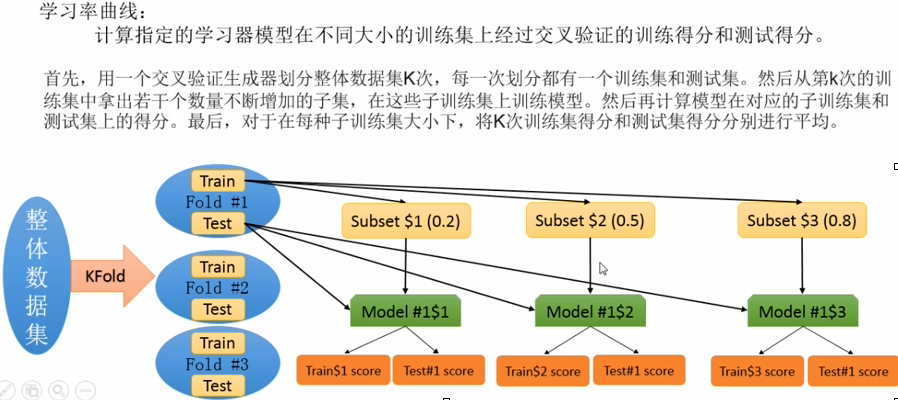
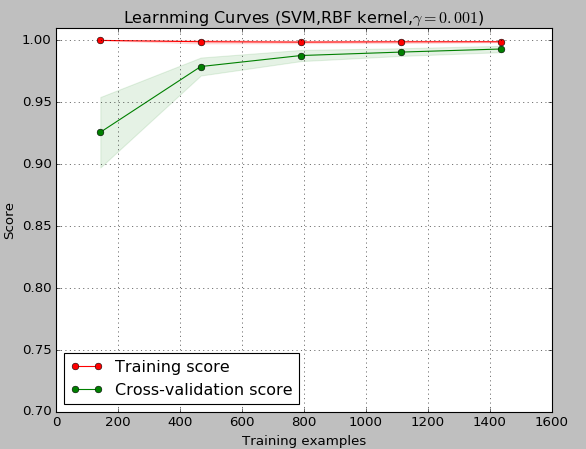
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.naive_bayes import GaussianNBfrom sklearn.svm import SVCfrom sklearn.datasets import load_digitsfrom sklearn.model_selection import learning_curvefrom sklearn.model_selection import ShuffleSplitdef plt_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_size=np.linspace(.1,1.0,5)):    plt.figure()    plt.title(title)    if ylim is not None:        plt.ylim(*ylim)    plt.xlabel("Training examples")    plt.ylabel("Score")    train_sizes,train_scores,test_scores=learning_curve(        estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_size)    train_scores_mean=np.mean(train_scores,axis=1)    train_scores_std=np.std(train_scores,axis=1)    test_scores_mean=np.mean(test_scores,axis=1)    test_scores_std=np.std(test_scores,axis=1)    plt.grid()    plt.fill_between(train_sizes,train_scores_mean-train_scores_std,train_scores_mean+train_scores_std,alpha=0.1,color="r")    plt.fill_between(train_sizes,test_scores_mean-test_scores_std,test_scores_mean+test_scores_std,alpha=0.1,color="g")    plt.plot(train_sizes,train_scores_mean,"o-",color="r",label="Training score")    plt.plot(train_sizes,test_scores_mean,"o-",color="g",label="Cross-validation score")    plt.legend(loc="best")    return pltdigits=load_digits()X,y=digits.data,digits.targettitle="Learning Curves(Nativr Bayes)"cv=ShuffleSplit(n_splits=100,test_size=0.2,random_state=0)estimator=GaussianNB()plt_learning_curve(estimator,title,X,y,ylim=(0.7,1.0),cv=cv,n_jobs=1)title="Learnming Curves (SVM,RBF kernel,$\gamma=0.001$)"cv=ShuffleSplit(n_splits=10,test_size=0.2,random_state=0)estimator=SVC(gamma=0.001)plt_learning_curve(estimator,title,X,y,(0.7,1.01),cv=cv,n_jobs=1)plt.show()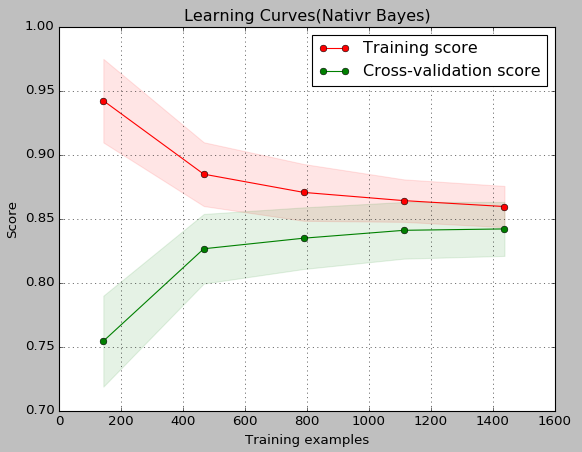

④、计算并绘制模型的验证曲线：model_selection.validation(estimator,...)

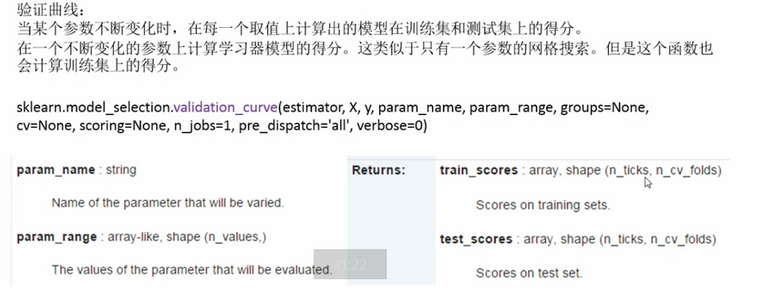
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.datasets import load_digitsfrom sklearn.svm import SVCfrom sklearn.model_selection import validation_curvedigits = load_digits()param_range=np.logspace(-6,-1,5)train_scores,test_scores=validation_curve(SVC(),X,y,param_name="gamma",param_range=param_range,                                          cv=10,scoring="accuracy",n_jobs=1)train_scores_mean=np.mean(train_scores,axis=1)train_scores_std=np.std(train_scores,axis=1)test_scores_mean=np.mean(test_scores,axis=1)test_scores_std=np.std(test_scores,axis=1)plt.title("Validation Curve with SVM")plt.xlabel("$\gamma$")plt.ylabel("Score")plt.ylim(0.0,1.1)lw=2plt.semilogx(param_range,train_scores_mean,label="Training score",color="darkorange",lw=lw)plt.fill_between(param_range,train_scores_mean-train_scores_std,train_scores_mean+train_scores_std,                 alpha=0.2,color="darkorange",lw=lw)plt.semilogx(param_range,test_scores_mean,label="Cross-validation Score",color="navy",lw=lw)plt.fill_between(param_range,test_scores_mean-test_scores_std,test_scores_mean+test_scores_std,                 alpha=0.2,color="navy",lw=lw)plt.legend(loc="best")plt.show()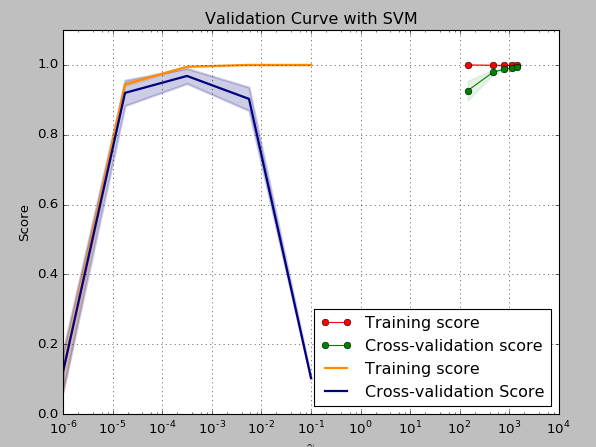

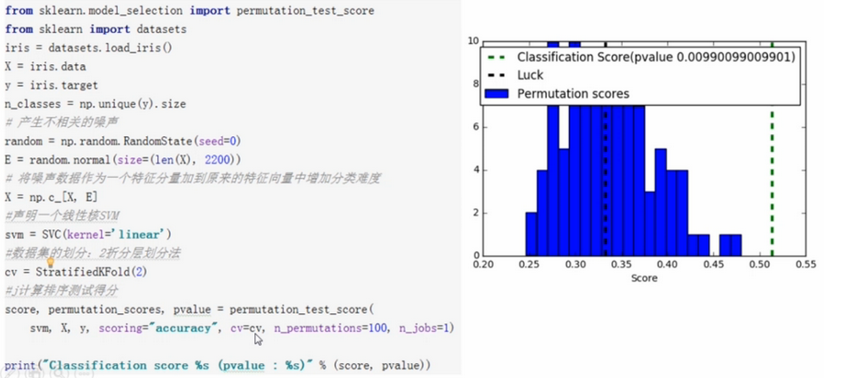
⑤、通过排序评估交叉验证的得分在重要性：model_selection.permutation_test_score(...)---现在用的很少

二、模型评估方法

sklearn模型预测性能的评估方法

Estimator对象的score方法

在交叉验证中使用的scoring参数

Estimator对象的score方法

score(self,X,y,y_true)函数在内部会调用predict函数获得预测响应y_predict,然后与传人的真实响应进行比较，计算得分

使用estimator的score函数来苹果模型的性能，默认情况下

分类器对应于准确率：sklearn.metrics.accuracy_score

回归器对应于R2得分：sklearn.metrics.r2_score

在交叉验证中使用scoring参数

上面的两个模型选择工具中都有一个参数“scoring”，该参数用来指定在进行网格搜索或计算交叉验证得分的时候，用什么标砖度量“estimator”的预测性能。默认情况下，该参数为“None”就表示“GridSearchCV”与“cross_val_score”都会去调用“estimator”自己的“score”函数，我们也可以为“scoring”参数指定别的性能度量标准，他必须是一个可调用对象，sklearn.metric不仅为我们提供了一系列预定义的可调用对象，而且好支持自定义评估标准。

在交叉验证中使用预定义scoring参数：

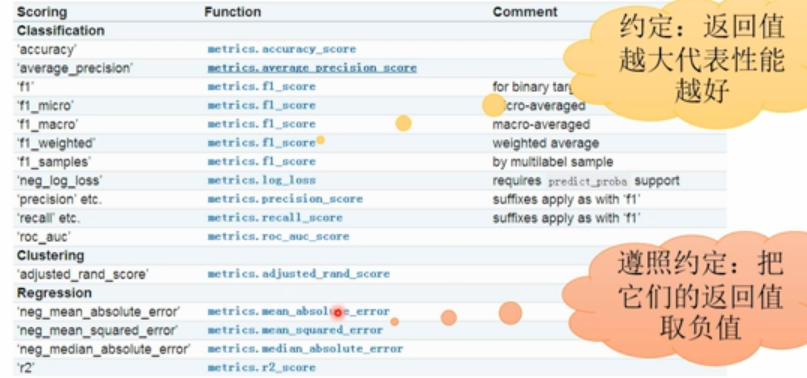
#在交叉验证中使用预定义scoring参数

from sklearn import svm,datasetsfrom sklearn.model_selection import cross_val_scoreiris=datasets.load_iris()X,y=iris.data,iris.targetclf=svm.SVC(probability=True,random_state=0)print(cross_val_score(clf,X,y,scoring="neg_log_loss")) #结果[-0.0757138  -0.16816241 -0.07091847] model=svm.SVC()print(cross_val_score(model,X,y,scoring="wrong_choice")) #结果：

ValueError: 'wrong_choice' is not a valid scoring value. Valid options are ['accuracy', 'adjusted_rand_score', 'average_precision', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_squared_error', 'neg_median_absolute_error', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc']

”scoring“的可用类型都存放在sklearn.metric.SCORES字典对象中

在交叉验证中海可以使用自定义scoring参数，具体讲解在

三、sklearn分类器评估指标总体概况

使用sklearn.metric包中的性能度量函数有：

分类器性能指标

回归器性能指标

聚类其性能指标

两两距离测度

分类器性能度量指标

总的来说，主要分为以下3类

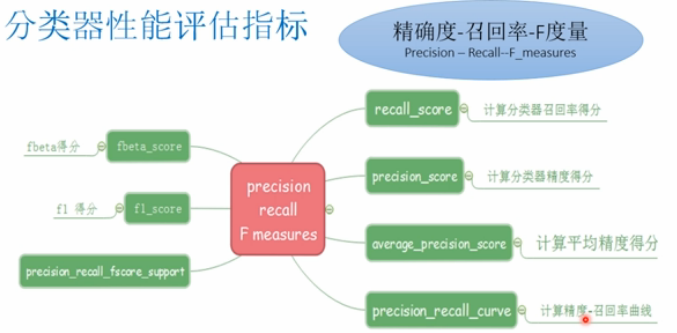
精度-召回率-F度量：Precision-Recall-F_measures

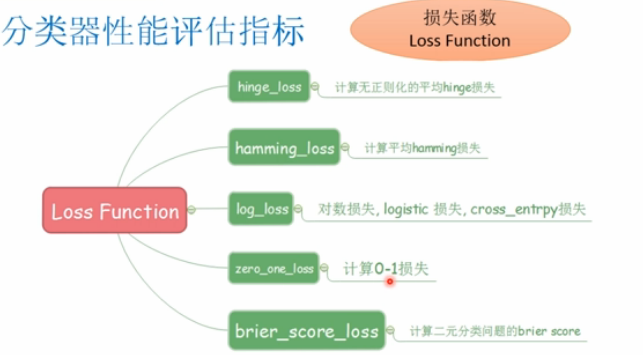
损失函数：Loss Function

接收机操作曲线：ROC Curves

只限于二分类单标签分类问题的评估指标

matthews_corrcoef(y_true,y_pred[],...):计算二元分类中的Matthews相关系数（MCC）

precision_recall_curve(y_true,probas_pred)：在不同的概率阈值下计算precision-recall点，形成曲线

roc_curve(y_true,y_score[,pos_label,...]):计算ROC曲线

可用于二分类多标签分类问题的评估指标

average_precision_score(y_true,y_score[,...]) 计算预测得分的平均精度（mAP）

roc_auc_score(y_true,y_score[,average,...])计算预测得分的AUC值

可用于多分类问题的评估指标（紫色的可用于多标签分类问题）

cohen_kappa_score(y1,y2[,labels,weights])

confusion_matrix(y_true,y_pred[,labels,...])

hinge_loss(y_true,pred_decision[,labels,...])

accuracy_score(y_true,y_pred[,normalize,...])

classification_report(y_true,y_pred[,...])

f1_score(y_true,y_pres[,labels,...])

fbeta_score(y_true,,y_pres,beta[,labels,...])

hamming_loss(y_true,y_pres[,labels,...])

jaccard_similarity_score(y_true,y_pres[,...])

log_loss(y_true,y_pres[,eps,normalize,...])

zero_one_loss(y_true,y_pres[,normalize,...])

precision_recall_fsconfe_support(y_true,y_pres)

多分类性能评估指标

将二分类指标拓展到多分类或多标签问题中：

分类器性能评估指标：

接收机操作曲线Reciever Operating Curves-》可用于二分类问题

解卡德指数（相似性系数）Jaccard similarity coefficient-》可用于多分类问题

MCC指标（相关性系数）Matthews correlation coefficient-》可用于二分类问题

四、分类器评估标准

准确率：返回被正确分类的样本比例（default）或者数量（normalize=False）

#准确率import numpy as npfrom sklearn.metrics import accuracy_scorey_pred=[0,2,1,3]y_true=[0,1,2,3]print(accuracy_score(y_true,y_pred))print(accuracy_score(y_true,y_pred,normalize=False))#0.5#2

混淆矩阵

from sklearn.metrics import confusion_matrixy_true=[2,0,2,2,0,1]y_pred=[0,0,2,2,0,2]print(confusion_matrix(y_true,y_pred))y_true=["cat","ant","cat","cat","ant","bird"]y_pred=["ant","ant","cat","cat","ant","cat"]print(confusion_matrix(y_true,y_pred,labels=["ant","cat","bird"]))#[[2 0 0][0 0 1][1 0 2]] #[[2 0 0][1 2 0][0 1 0]]

二元分类问题：

#precision-recall-F-measuresfrom sklearn import metricsy_pred=[0,1,0,0]y_true=[0,1,0,1]print(metrics.precision_score(y_true,y_pred))#1.0print(metrics.recall_score(y_true,y_pred))#0.5print(metrics.f1_score(y_true,y_pred))#0.666666666667print(metrics.fbeta_score(y_true,y_pred,beta=0.5))#0.833333333333print(metrics.fbeta_score(y_true,y_pred,beta=1))#0.666666666667print(metrics.fbeta_score(y_true,y_pred,beta=2))#0.555555555556print(metrics.precision_recall_fscore_support(y_true,y_pred,beta=0.5))#(array([ 0.66666667,  1.        ]), array([ 1. ,  0.5]), array([ 0.71428571,  0.83333333]), array([2, 2], dtype=int32))import numpy as npfrom sklearn.metrics import precision_recall_curvefrom sklearn.metrics import average_precision_scorey_true=np.array([0,0,1,1])y_score=np.array([0.1,0.4,0.35,0.8])precision,recall,threahold=precision_recall_curve(y_true,y_score)print(precision)#[ 0.66666667  0.5         1.          1.        ]print(recall)[ 1.   0.5  0.5  0. ]print(threahold)#[ 0.35  0.4   0.8 ]print(average_precision_score(y_true,y_score))#0.791666666667

多类别多标签分类问题

把其中的一类看成是正类，其他所有类看成是负类，每一类都可以看作是正类是都可以产生P，R，F，此时，可以按照5中方式来组合每一个类的结果，这5种方式是：macro，weighted，micro，samples，average=None

from sklearn import metricsy_true=[0,1,2,0,1,2]y_pred=[0,2,1,0,0,1]print(metrics.precision_score(y_true,y_pred,average="macro")) #0.222222222222 print(metrics.recall_score(y_true,y_pred,average="micro")) #0.333333333333 print(metrics.f1_score(y_true,y_pred,average="weighted")) #0.266666666667 print(metrics.fbeta_score(y_true,y_pred,average="macro",beta=0.5)) #0.238095238095 print(metrics.precision_recall_fscore_support(y_true,y_pred,beta=0.5,average="None")) #(array([ 0.66666667, 0. , 0. ]), array([ 1., 0., 0.]), array([ 0.71428571, 0. , 0. ]), array([2, 2, 2], dtype=int32)) print(metrics.recall_score(y_true,y_pred,average="micro",labels=[1,2])) #0.0

from sklearn.metrics import classification_reporty_true=[0,1,2,0,1,2]y_pred=[0,2,1,0,0,1]target_names=["class0","class1","class2"]print(classification_report(y_true,y_pred,target_names=target_names))

结果为：

precision recall f1-score support

class0 0.67 1.00 0.80 2

class1 0.00 0.00 0.00 2

class2 0.00 0.00 0.00 2

avg / total 0.22 0.33 0.27 6

Roc曲线

更多ROC曲线内容：spm=a2h0k.8191407.0.0&from=s1.8-1-1.2

ROC曲线只需知道true positive rate（TPR）和false positive rate（FPR），TPR，FPR被看作是分类器的某个参数的函数。

TPR定义了在全部的正样本中，分类器找到了多少个真真的正样本

FPR定义了在全部的负样本中，分类器把多少负样本错误的分为正样本

转载地址：http://yzvpx.baihongyu.com/